赌徒输光定理带给扑克人的启发（深度）part1：https://www.moshike.com/a/528.html

4

扑克中每个行为都有相应的EV

无论实在生活还是工作中，我们都希望德扑规则对自已的每一项投资得到相应的回报，而这种期望值就是你可以计算的最终的平均价值，这种预期价值我们简称为EV。扑克中每个行为都有相应的EV，EV是正的，长期来看就盈利，EV是负的，长期来看就在亏钱。

举例:你的底牌就是：A♠-2♠

而转牌后出来桌面上有 6♠-K♠-9♥-3♦

你有nuts同花面，彩池目前有50个筹码，而你正面对一个紧凑型（TP）的对手。但是现在你只有20个筹码，而你的对手还有很多筹码。此时他下注了20个筹码，你必须用所有的筹码来跟。从他的打法来看，你相信他手里一定有非常好的牌，至少是两对或三条。但是你的选择却只有跟牌或弃牌。这个时候你应该怎么做？

其实无论你怎么做，这局牌都结束了。你的输赢取决于河牌是什么。如果是黑桃，你就赢了，如果不是黑桃，那么你就输了。为了这样一个决定，就需要我们要计算每种打法的期望值，然后选择期望值较高的打法，这样才使得自己的获得更大的收益。

首先我们从弃牌分析，如果你弃牌你将没有任何损失也不会得到任何收益，所以你的期望值是0。

现在我们看看你跟注的情况，这或许有点复杂，一副扑克牌中有13张黑桃，现在你只看到了4张，其中两张在你手上，剩下的两张在桌面上。扑克牌一共52张，你看到其中6张，你意味着还剩46张没有出现，其中9张黑桃，37张是其他花色。

所以出现黑桃赢的概率是19.6%0.196=9/46

出现黑桃输的概率是80.4%

0.804=37/46

这两个数近似为20%和80%。在德扑圈里，我们的计算很少做到精准。所以我们只需要算出大概的近似值，通常情况下，这种近似值能带给我们的精确值一样的答案。

20%的情况，我们会赢，得到了70个筹码（彩池里的50个筹码加上对手的20个筹码）。平均一个，你能赢14个筹码。

14=20%*70

我们输的时候会输20个筹码。平均一下，我们损失了16……个筹码。

-16=-80%*20

现在我们期望值。因为跟牌后有两种可能，即-2个筹码。

-2=-16（输的时候）+14（赢得时候）

也就是说，每次跟注都要输掉两个筹码。

那么现在就有一个之前遗留下来的问题：跟注还是弃牌？跟注每次损失两个筹码，弃牌不损失，所以弃牌更好。弃牌不会赢钱，但是可以输的更少。

5

一个常见的术语误解

我们必须注意一个常见的术语误解。EV和全压EV（All in EV）并非一回事。前者是你预期从你的任何扑克决定那儿赢得而输掉的资金，不管牌局是否打到摊牌。后者仅指当一手牌打到摊牌时你的预期盈利，它是单单那种情况下的EV估量。

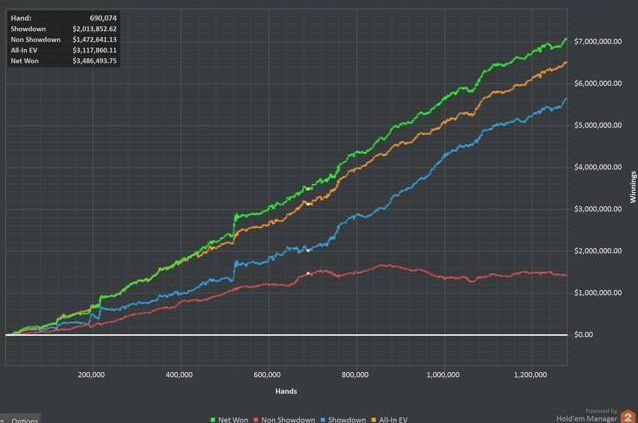
全压EV往往与实际金钱收益相比较，作为一种评估一名牌手有多幸运/不幸的指标。全压EV只是一幅描述牌手在一种情况下的波动的图片，它没有考虑许多牌手没有打到摊牌场合的运气，因此它远非一幅描述牌手究竟运气如何的全景图，大家不要太注重这个数据。

6

扑克中的波动

职业牌手往往将他们的职业描述为“一种费力不赚钱的谋生手段”。他们最头痛的一个问题是——必须应对收入的不稳定性。虽然使用了高效的技能组合，而且有多年的牌场经验，但许多牌手仍然回家时口袋中的钞票比上桌之前少。这种扑克中的资金起伏被牌手们一致称为“波动”（variance）。

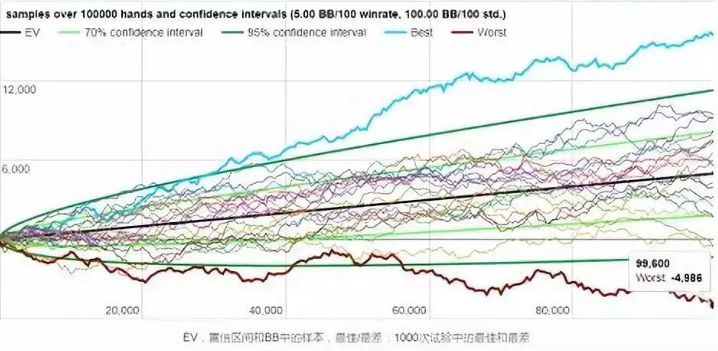
赌徒输光定理深度解析part3：https://www.moshike.com/a/546.html

WPT Global Taiwan 玩撲克贏真錢

本網站僅收集相關文章。如需查看原文，請複製並打開以下連結：赌徒输光定理深度解读part2